精选推荐 ▏学会旗舰会刊《CSIAM Transactions on Applied Mathematics》2025年精选文章推荐(三)
《CSIAM Transactions on Applied Mathematics》(CSIAM-AM)是中国工业与应用数学学会的旗舰期刊。该期刊发表应用数学、计算数学或科学计算领域的高质量原创研究论文。CSIAM-AM由中国工业与应用数学学会前任理事长、武汉大学校长张平文院士担任主编,中国工业与应用数学学会理事长、浙江大学求是讲席教授包刚院士担任总编辑。
2025年,CSIAM-AM刊发学术论文28篇。本期再推荐最后三篇精选文章,诚邀学界同仁及全球读者阅读、下载、引用。
01
Xiangcheng Zheng
CSIAM Trans. Appl. Math., 6(4), 666-710.
DOI: https://doi.org/10.4208/csiam-am.SO-2024-0052
文章介绍:
非局部算子是描述记忆效应和长程交互作用等时空非局部机制的重要数学工具,而变指数非局部算子能够简单有效地刻画非局部机制的时空非均匀性和多尺度特征,在吻合实验数据的情况下提升模型可计算性。同时,变指数的引入能够在局部消除传统非局部模型解的奇异性,具有重要理论价值。然而,变指数非局部算子无法通过积分变换等解析方法直接处理,也难以证明其具备强制性等良好性质,这为理论研究带来很大困难。对此,本文以变指数次扩散、超扩散等典型问题为例,提出了从外部引入辅助卷积核的卷积法以及从内部分裂核函数的摄动法,将以变指数非局部算子为主项的模型转化为具有简单主项的等价形式,从而在模型适定性与正则性、参数反演问题、数值格式收敛性等多个方面给出分析结果。本文所提方法思路新颖、普适性强,能够为多角度研究各类变指数非局部问题提供关键支撑,为模型应用提供理论基础。
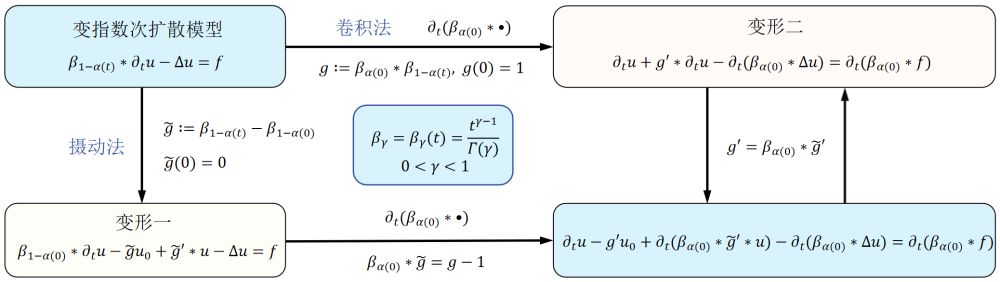
图1 示意图
02
A Sharp Uniform-in-Time Error Estimate for Stochastic Gradient Langevin Dynamics
Lei Li, Yuliang Wang
CSIAM Trans. Appl. Math., 6(4), 711-759.
DOI: https://doi.org/10.4208/csiam-am.SO-2024-0039
文章介绍:
在高维空间中抽取随机样本是许多科学与工程问题中一个重要而具有挑战性的问题。 随机梯度朗之万动力学(SGLD)是近年来广泛使用的抽样算法,通过将朗之万方程与随机分批思想结合,有效节约了计算成本。其采样误差估计一直是一个研究热点,然而现有结果一般使用轨道耦合方法,无法得到最精确的估计。
本研究提出了一套基于分布演化与相对熵的分析框架,证明了SGLD的时间一致、最优的误差界,对实际算法应用中的参数选取提供了重要指导。在证明中,我们通过Girsanov变换等工具,并对时间倒向条件期望进行细致分析,得到随机分批引入误差的精细估计。该分析框架具有较强的鲁棒性,可推广至随机微分方程多种数值方法以及随机多体系统的分析。目前已有相关工作基于此框架展开研究,显示其具有较大的扩展空间与应用潜力。
03
Tunan Kao, He Zhang, Lei Zhang, Jin Zhao
CSIAM Trans. Appl. Math.,6(4), 862-891.
DOI: https://doi.org/10.4208/csiam-am.SO-2024-0048
文章介绍:
求解含时偏微分方程是现代科学与工程计算领域的核心问题之一。近年来,以物理信息神经网络(PINN)为代表的深度学习方法,为高维问题的求解提供了新途径,但该类方法在时间外推能力与长时预测上仍存在局限;演化神经网络(EDNN)虽能更适配时间演化问题的求解,但其积分过程通常依赖蒙特卡洛方法,限制了整体求解精度。
为应对上述挑战,本研究提出部分演化张量神经网络(pETNNs)计算框架,核心优势体现在三方面:其一,利用张量神经网络(TNNs)的自变量分离结构,可通过高斯求积公式计算高维数值积分,既提升计算精度,又降低计算代价;其二,基于Dirac-Frenkel变分原理,将含时偏微分方程转化为关于网络参数的常微分方程,赋予模型优异的长时间预测能力;其三,依赖神经网络过参数化特性,引入部分参数更新机制,既能大幅降低计算成本,又能有效维持数值解的鲁棒性。
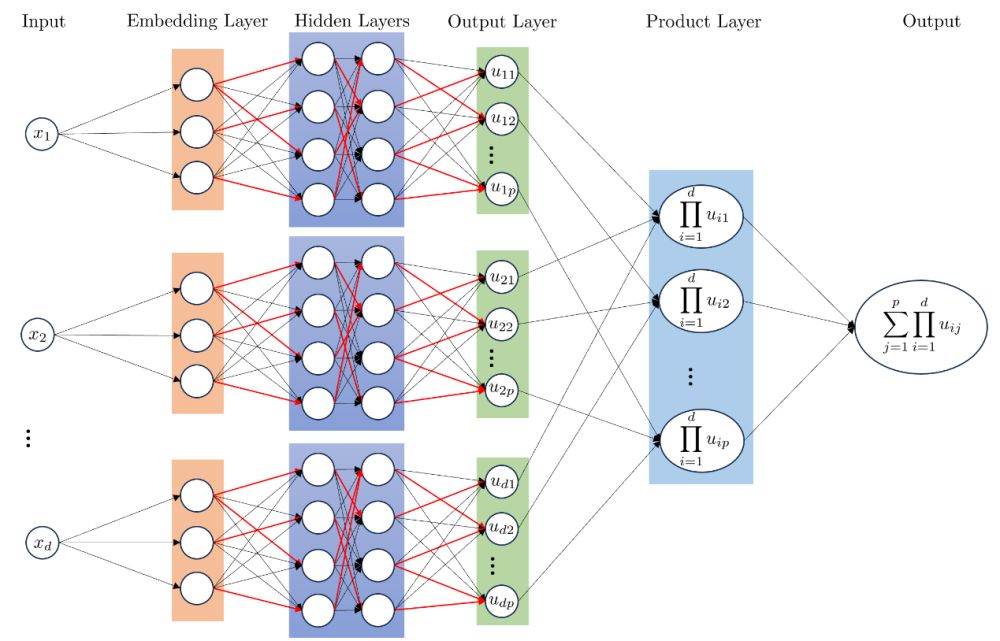
图2 pETNNs计算架构示意图。粗红线表示部分更新参数,嵌入层用于满足边界条件。
通过高维输运方程、热传导方程及Navier-Stokes方程等典型算例的数值实验,充分验证了该方法的优越性。本研究提出的pETNNs框架属于无网格参数化动力学近似方法,不仅为高维含时偏微分方程的求解提供了高效且稳定的新途径,也为深度神经网络的参数更新策略提供了创新性思路。
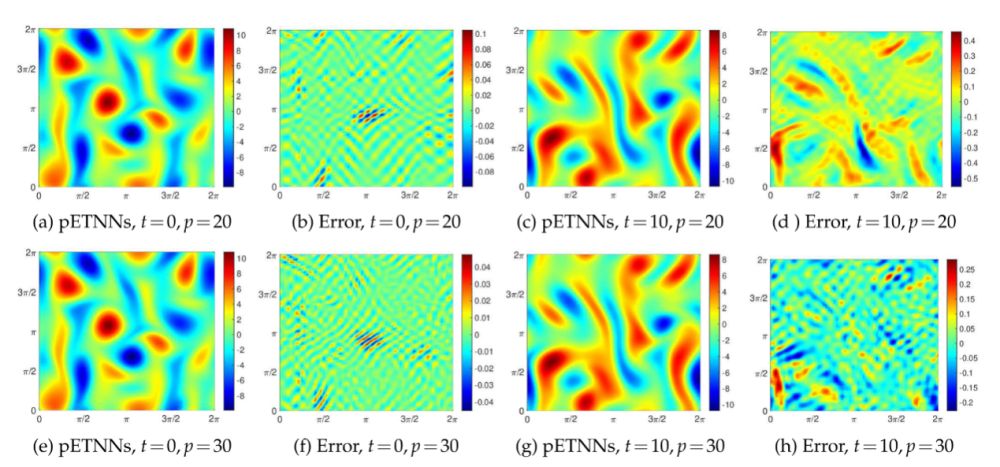
图3 pETNNs求解Navier-Stokes方程的数值解与误差分布(t=0, 10)。图(a)-(d)与(e)-(h)分别对应张量网络秩p=20与p=30的情形。
期刊官网:https://global-sci.org/index.php/csiam-am。
《CSIAM Transactions on Applied Mathematics》欢迎大家积极投稿,投稿网址: https://mc03.manuscriptcentral.com/csiam。
学会出版委员会供稿




